«Теория Стайна» это серия заметок, основанная на выкладках доктора прикладной теории вероятностей, Майка Стайна. Помимо прочих увлекательных исследований, в конце 2012-го господин Стайн отметился впечатляющим теоритическим трудом на тему, пожалуй, одного из самого злободневного вопроса в области всеми любимой карточной игры: и все же, покер это мастерство или удача?
← К предыдущей части (1): Преобладания
* * *
Методы анализа, основанные на конечных результатах
Подавляющее большинство способов определения влияния удачи и мастерства в покере опирается на эмпирические данные результатов смоделированных или настоящих игр. В этом смысле мы часто слышим о теоритических исследованиях, направленных на выяснение, скажем, различий между результатами лучших в своём классе игроков, или, например, определение математического ожидания ставки и влияния дисперсии на неё в долгосрочной перспективе.
Подобные исследования всегда основываются на сравнении конечных результатов, поэтому мы можем использовать их в качестве инструмента для определения мастерства и удачи в играх. То есть если в одной игре у каждого её участника практически равные шансы на победу (как в подбрасывании монетки), то это означает, что в такой игре преобладает элемент удачи. Но если один игрок способен побеждать в той или иной игре почти в 100% случаев благодаря своим навыкам (как в шахматах), то такая игра определённо будет «игрой мастерства».
Многие исследования подобного рода это достойная инвестиция времени её создателей. Но планируя использовать их в изучении покера, мы обязаны соблюдать предельную осторожность и помнить, что результат таких исследований полностью зависит от мастерства игроков отдельно взятой выборки. Другими словами, если все игроки в анализируемой базе будут иметь одинаковый уровень мастерства, а также/или будут использовать схожие стратегии, то сравнивая конечные результаты — мы едва ли сможем отличить симметричную высокоуровневую игру от подбрасывания монетки.
Для примера возьмём шахматы, квинтэссенцию игр мастерства: если за двумя столами встретятся две пары, в состав одной из которых войдут два титулованных гроссмейстера, а вторая включит в себя двух новичков, только вчера научившихся отличать пешку от ферзя, — исход встреч обеих пар будет складываться примерно 50/50.
Если же говорить о покере, то допустим, что в соответствии с какой-либо теорией, основанной на конечных результатах, лимит $1/$2 NL будет определен как «игра с незначительным преобладанием мастерства». Это не надуманный вывод, а результат систематического исследования указанного нами лимита: импровизированное исследование гласит, что на NL200 регуляров больше, чем на любом из предшествующих лимитов, а значит — сравнительно одинаковые винрейты тут будут встречаться чаще.
Таким образом, обозревая игру на ставках $10/$20 NL, наша система анализа конечных результатов должна будет заключить, что в отличие от NL200 здесь вообще нет элемента мастерства. Очевидно, что количество регуляров на $10/$20 NL значительно выше, чем на $1/$2 NL, но именно поэтому различия между винрейтами тут будет существенно ниже. И чем выше по лимитам мы будем подниматься, тем менее явным будет это различие. И в то же время покер остаётся покером вне зависимости от лимита, как же тогда объяснить, что на $1/$2 мастерства больше, чем на $10/$20?
Методы анализа, основанные на конечных результатах, могут классифицировать партию между «профессионалом» и «любителем», но не в силах определить долю мастерства или удачи, если уровень оппонентов – одинаковый.
Теоритически, влияние мастерства и удачи в игре не может меняться в зависимости от качеств её участника. Ведь мастерство и удача это неотъемлемые качества, которые будут существовать вне зависимости от действий игрока. Например, если два участника игры будут ходить случайным образом, совершенно не думая над своими действиями, то фактор мастерства в игре никуда не пропадёт – мастерство не исчезнет из дисциплины только потому, что в рамках отдельно взятой игры его решили не использовать. Если кто-то покупает смартфон, но решает использовать его только для звонков, то это не отменяет того факта, что заявленное устройство в самом деле смартфон.
Хотя эмпирическое доказательство и гласит: «Если участник той или иной игры, использующий некое стратегическое преимущество против одного оппонента, выигрывает более чем в половине случаев, то в такой игре существует элемент мастерства», – обратное утверждение будет ошибочным. Таким образом, в тех случаях, когда два игрока выигрывают друг у друга только в половине случаев, мы примем за действительность тот факт, что рассматриваемые игроки используют одну и ту же стратегию.
Обратите внимание, что игры, не включающие в себя элемент мастерства – яркий пример подобного утверждения. В таких играх стратегия никак не повлияет на результат, поэтому она всегда будет одинаковой.
Когда метод анализа, основанный на конечном результате в состоянии выявить тот факт, что умения игрока действительно влияют на результат его выступления в отдельно взятой игре, то это может служить доказательством наличия элемента мастерства в этой игре. Если же аналогичный метод анализа не в силах выявить зависимость прибыльности от умений, то это НЕ может быть доказательством отсутствия элемента мастерства в игре. И, тем не менее, иногда нас пытаются убедить в обратном; будьте осторожны – в определении влияния мастерства и удачи на ту или иную дисциплину нельзя полностью доверяться конечным результатам.
О намеренных проигрышах
В свое время Дэвид Склански популяризовал аргумент, в соответствии с которым покер является игрой мастерства потому, что «Игрок может проигрывать намеренно, если сидит за покерным столом, но никогда не сможет нарочно проиграть в рулетку, кости, игровые автоматы или лотерею». Этот лаконичный аргумент проводит чёткое различие между дисциплинами, подразумевающими стратегический элемент и казино гэмблингом, благодаря чему может служить неплохим инструментом при психологической обработке публики. Но может ли аргумент Дэвида Склански занимать более активную позицию в вопросе классификации игр?
В действительности, приведённый аргумент очень ограниченный и хрупкий. Если капнуть чуть глубже, то рулетка тоже может привести к намеренным потерям средств, если игрок нарочно заставит всё поле фишками из-за чего лишит себя возможности вернуть ставки даже в случае выигрыша. Более того, если верить аргументу господина Склански, то «Камень, ножницы, бумага» это азартная игра, потому как в ней не существует хода, ведущего к гарантированному поражению. Словом, всё, что способен раскрыть аргумент Дэвида Склански о какой-либо игре, так это наличие в ней стратегического элемента, влияющего на конечный результат. Поэтому я не думаю, что это изречение, некогда вычлененное великим игроком в покер, может быть использованы как-то иначе, нежели в качестве словесного украшения.
В попытке привязать идею Дэвида Склански к предмету определения преобладания элементов удачи и мастерства в покере, мы могли бы представить её в качестве научного исследования. В рамках этого исследования, по аналогии с работой «Об относительной мере мастерства для игр с элементами удачи», мы бы заставили новичка и эксперта независимо друг от друга сыграть в настольные казино игры (рулетку, например) и покер, при этом — фиксируя успеваемость участников эксперимента.
В любом варианте покера (то есть игре мастерства) результаты новичка и эксперта должны будут резко отличаться друг от друга и увеличиваться по мере набора дистанции, в то время как результаты обоих участников эксперимента за столом с рулеткой должны быть примерно схожими. В качестве дополнительного варианта проведения этого же исследования мы можем заменить новичка таким игроком, который будет принимать решения случайным образом. При этом, если покер это действительно игра мастерства – результаты обоих исследований не должны отличаться друг от друга. И вновь, демонстрация подобного различия может служить весомым аргументом в диалоге с широкой общественностью, так как оное определяет чёткую границу между играми, в которых стратегический элемент, а значит и уровень мастерства, оказывает на результат игры самое непосредственное влияние.
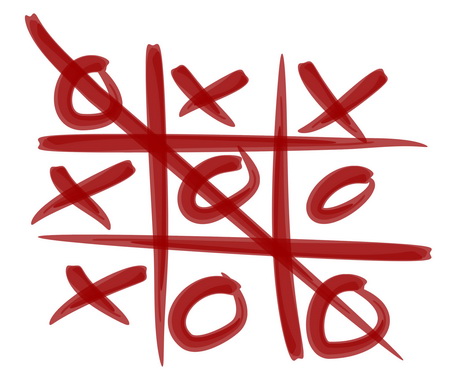
Но теоритическая последовательность приведённого нами метода может привести к довольно странной классификации некоторых игр. Для более детального объяснения этой туманной формулировки смоделируем гибрид из одной игры мастерства и одной игры удачи. Роль первой указанной пусть выполняет «Крестики-нолики», а второй – крэпс (игра в кости). Правила нашей новой игры, назовём её «Крестики-нолики-кубики», выглядят следующим образом: первый раунд это всегда крестики-нолики, и в том случае, если оный заканчивается ничьей, то игроки переходят за стол с крэпсом и бросают кубики, чтобы определить окончательного победителя. Аналогичным образом, если один из игроков побеждает ещё в первом раунде, то есть в крестики-нолики, то игра заканчивается, и до кубиков дело не доходит вообще. И поскольку в соответствии с выведенными нами ранее теориями, включая высказывание Дэвида Склански, игрой мастерства является любая дисциплина, в которой влияние на результат будет лежать на стратегическом элементе, то крестики-нолики-кубики будет считаться игрой мастерства, так как игрок может намеренно проигрывать первый раунд, тем самым снижая свою результативность.
Выходит, что если взять за основу шаблон «крестики-нолики-‘Х’», то игрой мастерства может стать совершенно любая многопользовательская дисциплина, вне зависимости от того, какую переменную мы будем использовать вместо ‘Х’. Разумеется, подобное утверждение не истинно, так что вся вышеизложенная теория это лишь необычный способ обернуть азартные игры в обложку игр мастерства.
Даже не прибегая к бессмысленному сшиванию игр, без сомнений, описанный подход сможет классифицировать в качестве игры мастерства совершенно любую симметричную многопользовательскую дисциплину, потому как практически любая такая дисциплина будет содержать пусть скудный и сумасбродный, но стратегический элемент.
А тем временем игра с откровенно плохой стратегической «поверхностью» не говорит ничего о других стратегических линиях или их комплексе в этой игре. Аналогичным образом худшая из возможных стратегий не раскрывает лучших стратегий в игре, и так далее. Поэтому подход, основанный на аргументе Дэвида Склански, не может быть применён для определения «стратегической глубины» в той или иной игре. С таким же успехом мы могли бы добавить в некоторые игры кнопку «Проиграть» и утверждать, что в игру был добавлен стратегический элемент, и поскольку теперь в неё можно проиграть нарочно – она стала игрой мастерства. Да, теперь в ней есть требование к умению игрока, и оно заключается в том, чтобы… никогда не нажимать кнопку «Проиграть»? Несомненно, чтобы выполнить это условие игроку понадобится какое-то мастерство, но только в очень ограниченном и непрактичном смысле.
Из всего вышесказанного мы можем заключить, что демонстрация худшей результативности худшего возможного игрока может отразить ТОЛЬКО ненулевое количество навыков в той или иной игре. И это предел подхода, основанного на аргументе Дэвида Склански.
Источник: http://www.pokeroff.ru
Комментарии